Basic Constructions

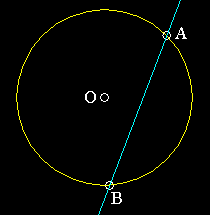
In geometric constructions, you need only four instruments: paper, pencil, a ruler or straightedge, and a compass (instrument used to draw circles). The diagrams you see were all created using AutoCAD 2002. They are very self explanatory. A large circle represents a circle drawn by a compass. A point is usually a very small circle. Circles are referred to by their centers, so in this case, this circle is called circle O. A line is only allowed to connect given points or intersections. They will be represented by a pair of letters with a line above them. So, the line in this diagram is called line AB.

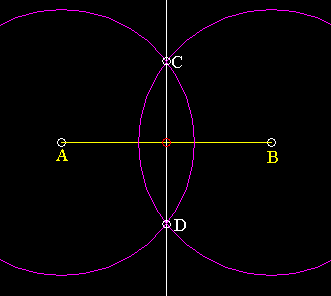
Line Bisection

The bisection of a line is one of the most fundamental of all geometric constructions. In this example, we construct the perpendicular bisector. Suppose you have line AB.
  1. Draw a circle at point A.
  2. Next, draw a circle at point B
  3. The two circles intersect at points C and D.
  4. Draw a line through points C and D.
  5. CD intersects AB at the midpoint.

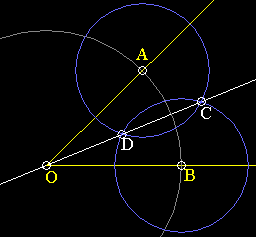
Angle Bisection

This section shows you the procedure to bisect any arbitrary angle. That is, given an angle, cut it in half exactly. So, given angle AOB:
  1. Construct a circle at point O with radius OA. This circle should intersect at points A and B.
  2. Draw a circle at points A and B. They must intersect each other at two points. Call them C and D.
  3. Draw a line through points C,D,O. This line bisects angle AOB.

Perpendiculars

We've seen how to contruct a perpendicular bisector. What if we want to construct a perpendicular line through any point? Given AB, we want to construct a perpendicular at point M:
  1. Draw a circle at M.
  2. Where the circle intersects AB, construct a perpendicular bisector.
Parallels
Suppose you want to construct a line parallel to a given line, through a given point. You would follow this procedure:
  1. Given line AB (yellow) and point C. We want to construct a line parallel to AB through C.
  2. Connect points A and C.
  3. Draw a circle at A (green), crossing C. Circle A (green) intersects AB at D.
  4. At points C and D, draw circles crossing point A (purple). These two circles intersect each other at E.
  5. Connect points C and E with a line. CE is parallel to AB!

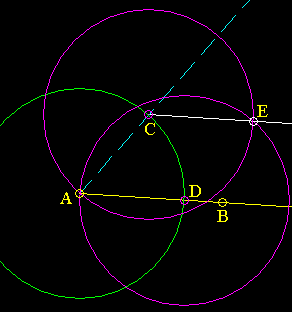
Mascheroni Bisection

A Mascheroni construction does not use a straightedge, making the bisection of a line ten times harder! You are given two points A and B:
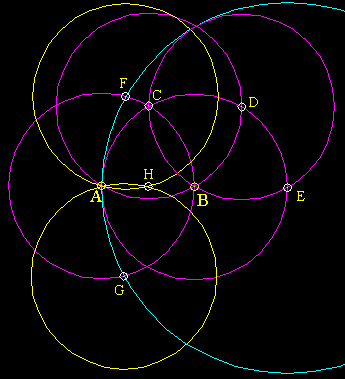
  1. Draw a circle at A and B (purple). They intersect at C. Draw an identical circle at C (purple), that intersects circle B at D. Draw an identical circle at D (purple) that intersects circle B at E.
  2. Draw a circle at E (cyan) so that it crosses A. It also intersects circle A at points F and G.
  3. Draw a circle at F and one at G (yellow), each crossing the point A. Their intersection H, is the midpoint of AB

© Apr. 2003 Robin Hu