Other Constructions

Line Trisection
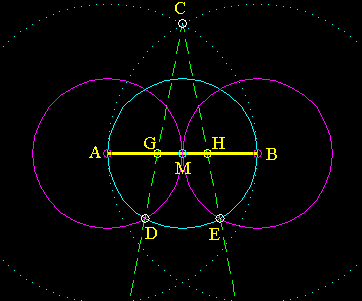
We are given a line (AB), and we want to cut it into three equal pieces. To do this:
  1. Find M the midpoint of AB.
  2. Draw a circle at A and B (dotted), each with radius AB. They cross each other at C.
  3. At points A and B, draw a circle (purple) crossing M.
  4. At point M, draw a circle (cyan) crossing A. Circle M (cyan) intersects circles A and B (purple) at points D and E.
  5. Draw a line through points CD and CE (green dashed).
  6. CD and CE intersect AB at points G and H.
  7. AG, GH, and HB are all 1/3 of AB.
Another method of line trisection doesn't involve that many circles, but rather a lot of lines! We are given segment AB (yellow):
  1. Draw a circle at A and a circle at B (dotted), each having a radius of AB. They cross each other at two points, C and D.
  2. Draw a line through points CA. CA (cyan) crosses circle A (dotted) at point E.
  3. Draw a line through points EB (red).
  4. Draw a line through points AD (magenta). AD (magenta) crosses EB (red) at point F.
  5. Draw a line through points CF. CF crosses AB at point G.
  6. AG is therefore 1/3 of AB!
Line Division
What if you needed to divide a line into an n number of parts, such as 5,7 or 11? The general construction for line division goes like this, given AB (yellow):
  1. Find any point P1 above AB. Draw a line through points A and P1.
  2. Find points P2...Pn where n is the number of segments you want to divide your line into (in this case,5). AP1=P1P2=...Pn-1Pn.
  3. Draw a line from Pn to B.
  4. Draw a line parallel to BPn from points Pn-1,Pn-2.... They cross AB at the points of n-section.

Square Roots

Using a compass and straightedge, it is even possible to construct the square root of any given line segment! We are given AB (yellow). In this example, it has a lenght of 3 and we want to construct the squareroot of 3.
  1. Extend AB. Find C on AB so that CA = 1.
  2. Find M, the midpoint of CB.
  3. Draw a circle at M (magenta) crossing C.
  4. From point A, draw a line perpendicular to it and find D, the intersection of that line with circle M (magenta).
  5. AD is therefore the squareroot of AB!
Quadrature of a Rectangle
The quadrature of a rectangle, is the construction of a square equal in area to a given rectangle. It is somewhat based on the construction for squareroots. Suppose we are given rectangle ABCD:
  1. Extend AB. Find E on AB so that BE = BC.
  2. Find M, the midpoint of AE.
  3. Draw a circle at M (cyan) crossing A.
  4. Draw a line from B (red) perpendicular to AB, crossing circle M (cyan) at N.
  5. BN is a side of the new square!

Quadrature of a Triangle

We already know how to square a rectangle. Then squaring a triangle should be no problem. Suppose we are given a triangle:
  1. Find the height of the triangle.
  2. Find a rectangle with equal area as the triangle (the rectangle has a height of half the height of the triangle and the same base).
  3. Square the rectangle.

      © Apr.7 2003 Robin Hu. All Rights Reserved.