The Heptagon

This first construction is the easiest. It is a very good approximation of the heptagon. Given circle O (yellow): Find A, a random point on the circle. Find the M, the midpoint of OA. Draw a perpendicular line through M. It intersects circle O at B. Draw a circle at B (cyan) so that it crosses M. Circle B intersects circle O at two points of the heptagon. You can use them to find the rest.

There is a method of approximating nearly any regular polygon with compass and straightedge. It is especially useful with odd shapes like heptagons and nonagons. They are difficult in that they involve the division of lines. Draw circle O. Draw AB, the diameter of circle O. Divide AB into n number of parts (n being the number of sides , in this case 7!). Draw two circles, one at A and one at B (cyan), each with radius AB. They intersect at C. Point D is the second point from the left of the diameter. Draw a line from C to D, extending it all the way to the original circle, where it intersects at E. A and E are two points of the heptagon. Use them to find the rest. You can use this approximate any n-gon!

This next construction was formulated by myself. It's not as accurate at the others, but it's relatively easy. Draw circle O. Draw OA and OB, so that they are perpendicular to each other and A and B are on circle O. Draw BC, so that it is perpendicular to AB (purple) and has half it's length. Draw a line through CA (cyan). Draw a circle at C so that it crosses B (red). Circle C (red) crosses CA (cyan) at D. At point A, draw a circle that crosses D. Circle A intersects circle O at two points of the heptagon.

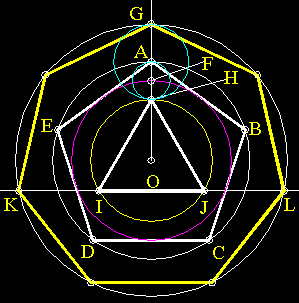
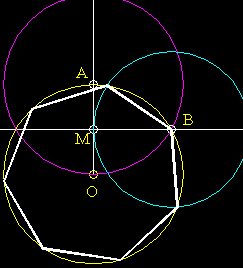
Here's a very complicated construction, yet very accurate. Draw circle O. Draw ABCDE, a pentagon inscribed in circle O. Draw another circle at O, this time inside the pentagon (purple). To do this, find the midpoint of one of the sides of the pentagon and draw a circle crossing that point. Draw OA. OA intersects the small circle (purple) at F. Draw a circle at F (cyan) that crosses A. It crosses OA at H. Draw a circle at A (cyan) that crosses H. Circle A (cyan) crosses OA at G. Draw a small circle at O (yellow) that crosses H. Inscribe an equilateral triangle, HIJ inside that circle (yellow). 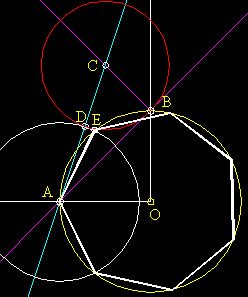Draw a line through points I and J. Draw a circle at O that crosses point G. This circle crosses IJ at points K and L. G,K,L are 3 points of the heptagon. Use them to find the rest!

See Nexusjournal for details

This is a new construction. It involves the use of a grid. Find point (2,4). Draw a circle centered at the origin crossing that point. Draw a line at y = -1. This line crosses the circle at two points of the heptagon.

Shown here is the Neusis Construction for a Heptagon, which involves a marked straightedge. You can find more info at Mathworld. Take a straightedge (such as a piece of paper) and mark two points on it, A and B. Construct segment CD which is equal to AB. Find the midpoint of CD and call it M. Draw a perpendicular bisector through point M. Draw segment CE so that CE is perpendicular to CD and is equal in length. Draw a circle centered at D and crossing point E. Take your marked straightedge and place it so that A is touching the arc, B is touching the perpendicular bisector of CD, and the straightedge is touching point C. Then angle CBM or q is equal to p/14. Thus, 4q will give you 2p/7, which is what we wanted!